Joint work with Santiago Pereda Fernández. Revision requested at Econometric Reviews.
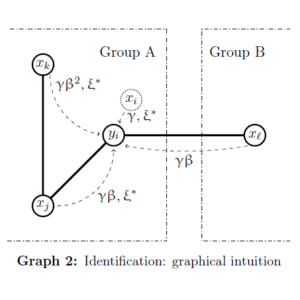 Abstract. Researchers interested in the estimation of peer and network effects, even if these are algebraically identified, still need to address the problem of correlated effects. In this paper we characterize the identification conditions for consistently estimating all the parameters of a spatially autoregressive or linear-in-means model when the structure of social or peer effects is exogenous, but the observed and unobserved characteristics of agents are cross-correlated over some given metric space. We show that identification is possible if the network of social interactions is non-overlapping up to enough degrees of separation, and the spatial matrix that characterizes the co-dependence of individual unobservables and peers’ characteristics is known up to a multiplicative constant. We propose a GMM approach for the estimation of the model’s parameters, and we evaluate its performance through Monte Carlo simulations. Finally, we show that in a classical empirical application about classmates our approach might estimate statistically non-significant peer effects when conventional approaches register them as significant.
Abstract. Researchers interested in the estimation of peer and network effects, even if these are algebraically identified, still need to address the problem of correlated effects. In this paper we characterize the identification conditions for consistently estimating all the parameters of a spatially autoregressive or linear-in-means model when the structure of social or peer effects is exogenous, but the observed and unobserved characteristics of agents are cross-correlated over some given metric space. We show that identification is possible if the network of social interactions is non-overlapping up to enough degrees of separation, and the spatial matrix that characterizes the co-dependence of individual unobservables and peers’ characteristics is known up to a multiplicative constant. We propose a GMM approach for the estimation of the model’s parameters, and we evaluate its performance through Monte Carlo simulations. Finally, we show that in a classical empirical application about classmates our approach might estimate statistically non-significant peer effects when conventional approaches register them as significant.